最近看到一些文章討論【Math. for programmers】，談到程式設計師要具備的數學素養，尤其是AI盛行後，許多數學與統計學科開始影響我們，例如下圖：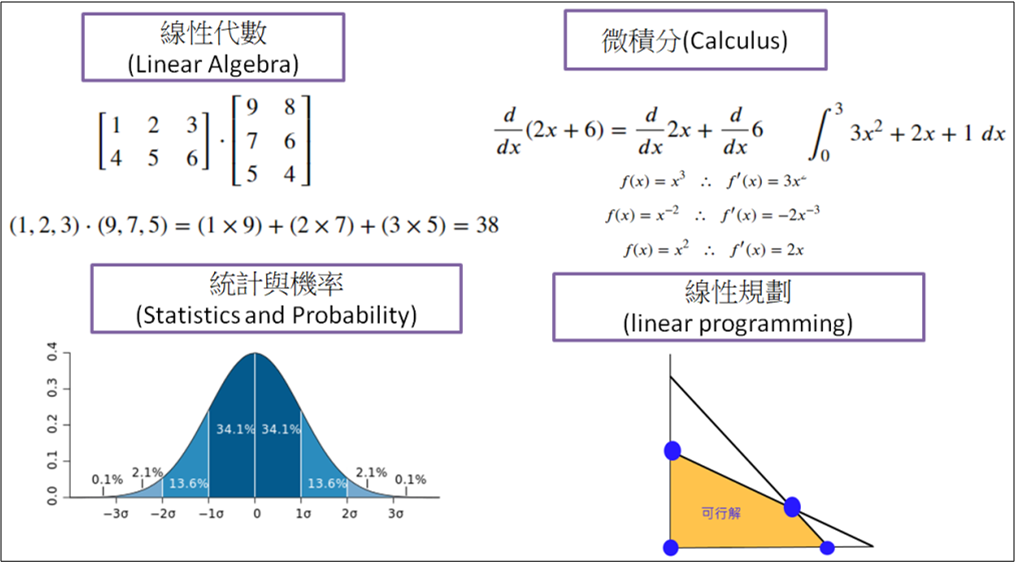

以機器學習/深度學習而言，我們至少需要熟悉以下學科：

1. 線性代數(Linear Algebra)
2. 微積分(Calculus)
3. 統計與機率(Statistics and Probability)
4. 線性規劃(linear programming)
5. 馬可夫決策過程(Markov decision process, MDP)
6. 時間序列分析(Time series analysis, TSA)
7. ...

以下筆者就舉一些範例說明數學的實用性。

線性代數(Linear Algebra)

線性代數的張量(Tensor)運算是深度學習的計算基礎，一維張量稱為向量，二維張量稱為矩陣，以下就舉一些範例說明線性代數可以解決的問題。本文主要使用NumPy及一些延伸的套件SymPy、SciPy...等，他們提供線性代數、微積分、統計、機率各方面的函數庫。

範例1. 利用矩陣求解聯立方程式(Systems of Equations)，程式名稱為30\Systems_of_Equations.py。

1. 有一聯立方程式如下，可以使用矩陣表示，並利用點積(Dot product)及反矩陣求解。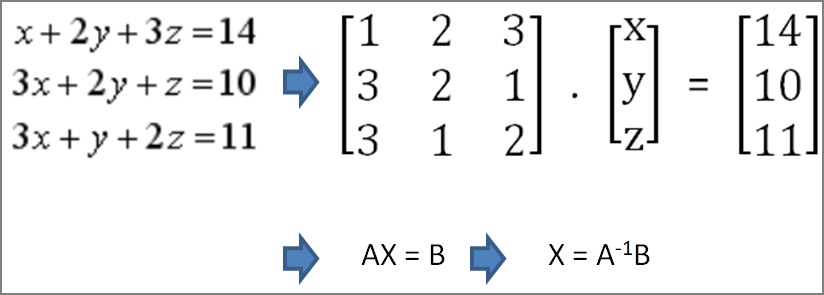
   

2. 程式碼：使用NumPy套件。

import numpy as np
a = np.array([[1, 2, 3], [3, 2, 1], [3, 1, 2]])
b = np.array([14, 10, 11])
print('method 1\n', np.linalg.inv(a) @ b) # X = A^(-1).B
# 驗證
print('method 2\n', np.linalg.solve(a, b))

3. 執行程式：

python Systems_of_Equations.py

4. 執行結果：驗證無誤。

method 1
 [1. 2. 3.]
method 2
 [1. 2. 3.]

範例2. 以最小平方法(OLS)求簡單線性迴歸(y=wx+b)參數(w、b)的公式，再以矩陣運算，程式名稱為30\regression1.py。

1. 須先安裝SciKit-Learn套件。

pip install scikit-learn

2. 程式採用隨機生成的資料集：

X_org, y = make_regression(n_samples=100, n_features=1, noise=15, random_state=42)

3. 使用上述公式求w、b，並以NumPy驗算，執行結果：答案相同，驗證無誤。

[45.78520483  1.74767298]
[45.78520483  1.74767298]

梯度下降法(Gradient Descent)

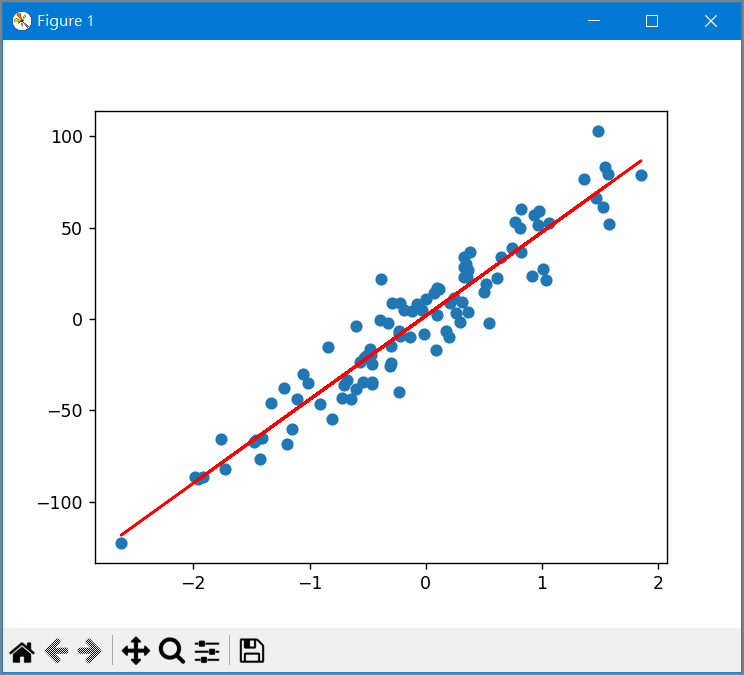
梯度下降法是神經網路(Neuron network)求解的精髓，面對複雜的模型我們無法利用數學公式求解，只能採用逼近求解的優化(Optimization)方式，要邁入深度學習必先瞭解此原理。

範例3. 利用梯度下降法(Gradient Descent)求最小值，程式名稱為30\gd1.py。梯度下降法詳細說明可參閱【進一步理解『梯度下降』(Gradient Descent)】。

1. 假設損失函數f(x)=x^2，可以使用微分計算梯度(斜率)，並沿著梯度往下走，可找到最小值。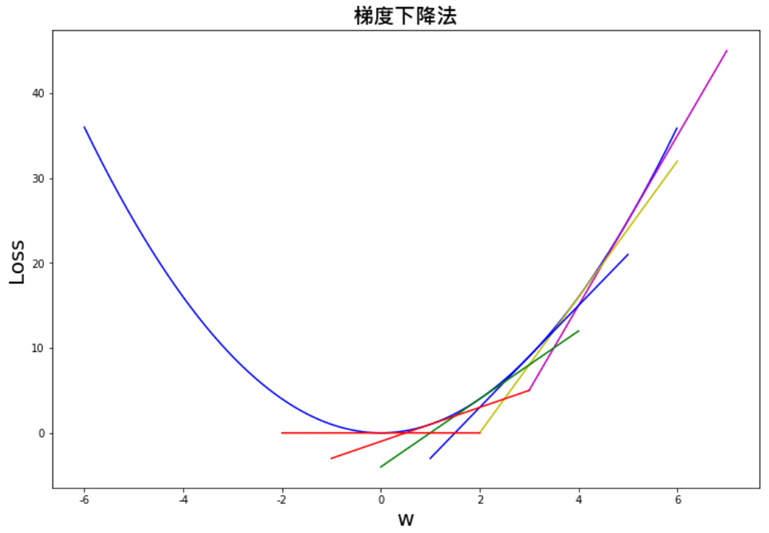
   

2. 引入套件，並定義損失函數及其一階導數。

import numpy as np
import matplotlib.pyplot as plt

# 損失函數:y=x^2
def func(x): return x ** 2 

# 損失函數的一階導數:dy/dx=2*x
def dfunc(x): return 2 * x

3. 梯度下降法：權重的更新公式為【新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)，執行N個執行週期(epochs)。

def GD(x_start, df, epochs, lr):    
    xs = np.zeros(epochs+1)    
    w = x_start    
    xs[0] = w    
    for i in range(epochs):         
        dx = df(w)        
        # 權重的更新 W_new = W — learning_rate * gradient        
        w += - dx * lr         
        xs[i+1] = w    
    return xs

4. 設定起始權重、執行週期數、學習率，執行梯度下降法。

# 超參數(Hyperparameters)
x_start = 5     # 起始權重
epochs = 15     # 執行週期數 
lr = 0.3        # 學習率 

# 梯度下降法 
# *** Function 可以直接當參數傳遞 ***
w = GD(x_start, dfunc, epochs, lr=lr) 
print (np.around(w, 2))

5. 執行程式：

python gd1.py

6. 執行結果：從起始點5，一直遞減，直至0後不再變化，故0即為最小值。

[5.   2.   0.8  0.32 0.13 0.05 0.02 0.01 0.   0.   0.   0.   0.   0.   0.   0.  ]

7. 可繪圖驗證。
   

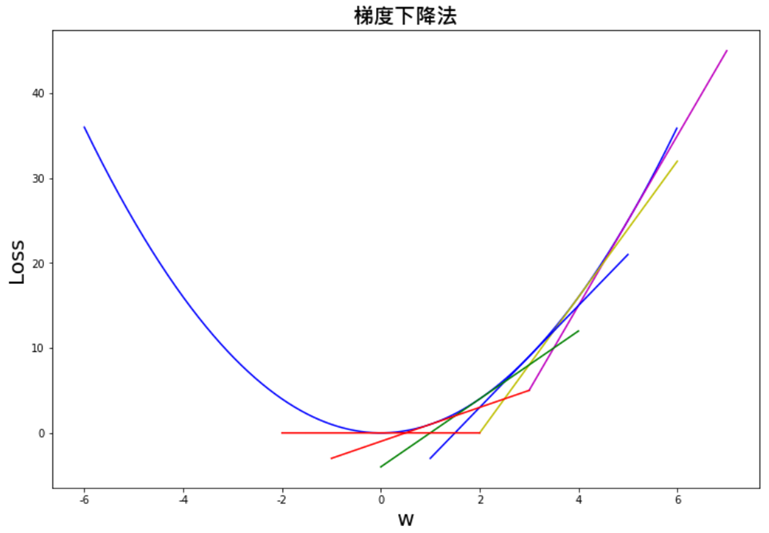
8. 也可以改變起始點(x_start)，例如-6，從損失函數的另一邊開始尋求最佳解，一樣可以得到最小值0。執行週期數、學習率也可以改變，實驗看看。

9. 若損失函數很複雜，可以使用SymPy套件進行微分，不必手動微分，完整程式碼請參見gd2.py。

from sympy import *

x = Symbol('x')
y = x ** 2 
yprime = y.diff(x)

# 損失函數:y=x^2
def func(x): return x ** 2 

# 損失函數的一階導數:dy/dx=2*x
def dfunc(x_value): return yprime.subs(x, x_value).evalf()

10. 讀者也可以使用較複雜的損失函數實驗看看，例如：

# 損失函數
def func(x): return 2*x**4-3*x+2*x-20

範例4. 應用梯度下降法(Gradient Descent)，把均方誤差(MSE)當作損失函數，力求它最小化，求簡單線性迴歸(y=wx+b)的參數(w、b)，程式名稱為30\regression_gd.py。相關數學原理可參閱【突破數學/統計魔障，打好AI學習基礎 -- 再戰梯度下降(1)】。

1. 程式碼較長，請直接參閱程式檔。
2. 執行結果：直接觀看【動畫】。
3. 其他的演算法，如支援向量機(SVM)、羅吉斯迴歸...等，都可以應用梯度下降法求解，只要訂定損失函數，其他幾乎不必修改。

機率(Probability)

機率(Probability)是機器學習推論的基礎原理，不管是預測或生成對話，都不會100%準確，而是在多個候選答案中取機率最大者為預測值。

範例5. 計算【今彩539】中獎機率，程式名稱為30\lotto1.py。

1. 【今彩539】遊戲規則如下：從1~39號碼抽5個，依猜中個數獲得1~4獎。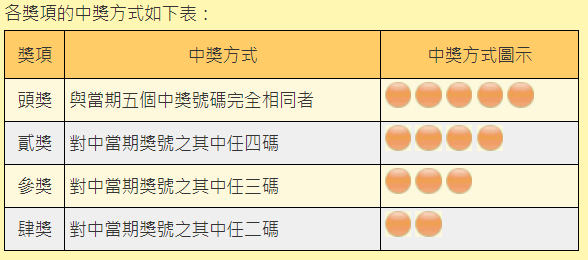
   

2. 中獎機率基本上是個組合(Combination)的問題，公式如下：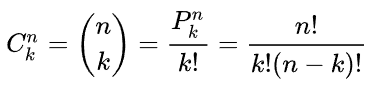
   

3. SciPy套件的sps.comb(n, k)函數可直接計算組合公式，例如二獎，5個中獎號碼猜中4個，34個未中獎號碼猜中1個，故二獎組數計算如下：

print('二獎組數：', sps.comb(5, 4)*sps.comb(34, 1))

4. 平均中獎金額計算如下：

# 各獎組數 
prize_count = np.array([sps.comb(5, 5)*sps.comb(34, 0), sps.comb(5, 4)*sps.comb(34, 1), 
                    sps.comb(5, 3)*sps.comb(34, 2), sps.comb(5, 2)*sps.comb(34, 3)])

# 中獎金額 
prize_amount = np.array([8000000, 20000, 300, 50])
            
# 平均中獎金額
print('平均中獎金額：', round(np.sum(prize_count*prize_amount) / sps.comb(39, 5), 2))

5. 執行結果：平均中獎金額只有27.92元，成本是50元，你覺得划算嗎?

馬可夫決策過程(Markov decision process, MDP)

由馬可夫決策過程演化而成的強化學習(Reinforcement learning, RL)，不只可以玩遊戲(AlphaGo)，還可解決很多商業問題，例如路徑規劃、庫存管理、機器人操作、股票投資...，甚至包括ChatGPT的模型訓練，以下舉個簡單範例【迷宮求解】。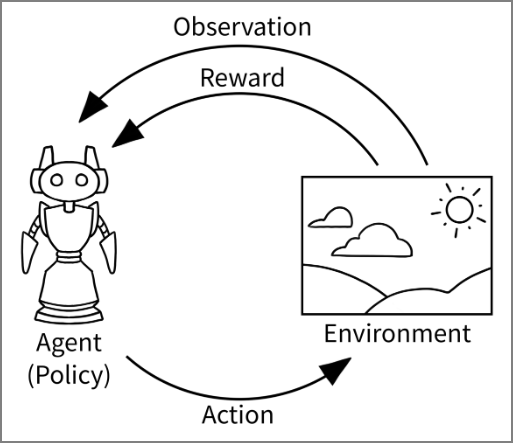

馬可夫決策過程，圖片來源：【Gymnasium Basic Usage】

範例6. 迷宮求解，程式名稱為30\Frozen_lake_test.ipynb。

1. 須先安裝gymnasium套件。

pip install gymnasium

2. 以Jupyter notebook或Jupyter lab執行Frozen_lake_test.ipynb。

3. 載入迷宮遊戲FrozenLake-v1，隨機行走測試，很難順利走到右下角終點。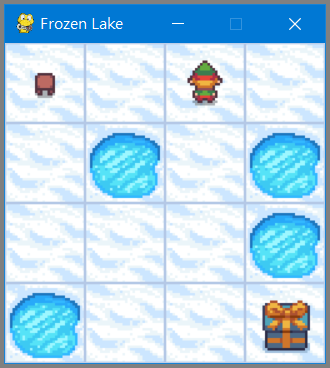
   

4. 利用動態規劃(Dynamic Programming)及Bellman方程式，訓練模型
   Bellman方程式: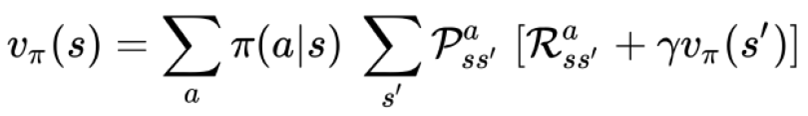
   

5. 執行結果：依照下方表格指示，比較目前位置的上/下/左/右的數值最大者行走。
   

6. 經過訓練之後，每次都可以順利走到終點。

結語

有些讀者可能會問【數學及演算法不是由資料科學家搞定嗎?】，是的，但是由非專業的開發人員撰寫程式，可能沒有能力應用本系列文章的各項設計典範或架構，使程式具備效能、彈性、擴充性...，因此，程式設計師還是要瞭解相關數學/統計，才能與資料科學家溝通，合力開發應用系統。

今年(2024)的諾貝爾物理獎竟然是由帶動第三波AI的大老Geoffrey Hinton獲得，更誇張的是，之後兩天公佈化學獎得主之一是Deepmind公司老闆Demis Hassabis，也是AlphaGo發明人，當然他不是因AlphaGo得獎，而是藉由強化學習開發【蛋白質結構預測】的AlphaFold模型。這兩個事件提醒我們，跨學科合作的時代已經來臨，程式設計師受到其他學門的衝擊會愈來愈大，未來這個職業可能要細分為數學程式設計師、物理程式設計師、化學程式設計師...等。

本系列文章主要探討【開發中大型應用系統的各項技能】，除了強迫筆者自我學習外，也希望透過分享，獲得同好更多的交流與指正，繼續 Happy coding 嘍 !!

本系列的程式碼會統一放在GitHub，本篇的程式放在src/30資料夾，歡迎讀者下載測試，如有錯誤或疏漏，請不吝指正。